In an HVAC cable, electric field distribution depends on capacitances, which are dominated by permittivity of the insulation material that is stable with temperature. A specified ∆θmax is therefore not required when testing such cables. By contrast, field distribution in an HVDC cable is determined by resistivity of the insulation material, which varies greatly with temperature. This results in the need to control temperature difference, ∆θmax, during thermal stresses represented by the load cycle in a test. In operation, an HVDC cable also experiences SI/LI overvoltage, which is superimposed onto the DC service voltage. As such, to properly simulate an in-service condition, superimposing a switching surge and a lightning transient onto the operating DC voltage is a standard requirement.
This edited past contribution to INMR by Hong He and W. Sloot of KEMA Labs in the Netherlands described a test circuit with two separate test systems – a DC generator and an impulse generator, connected with a test cable system located between the two. The test cable system consists of three pieces of 50 m HVDC XLPE cable assembled with two outdoor terminations and two joints. One major complexity from this arrangement is preventing damage to each test system due to presence of the other. Therefore, a sphere gap is installed to block DC voltage from the impulse generator with a damping impedance set to protect the DC generator from very fast transients.
Thermal Physical Model
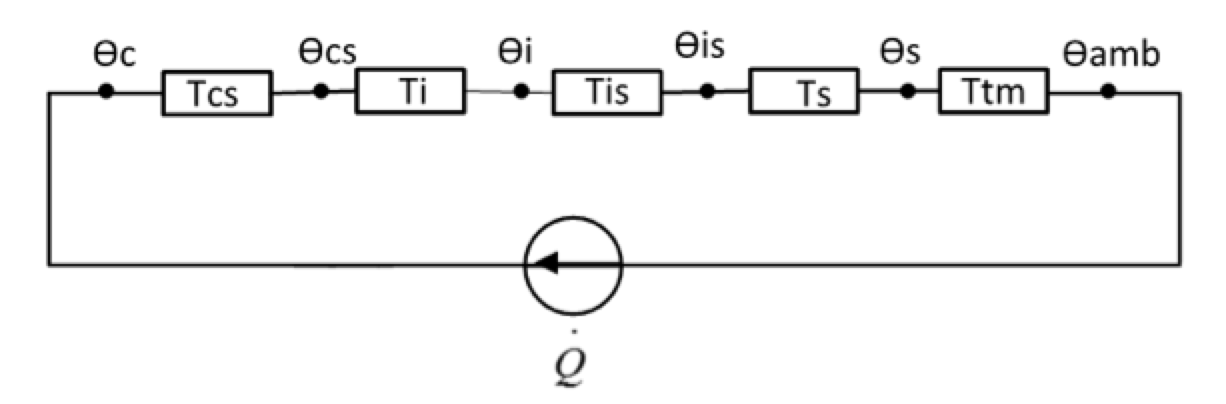
A temperature difference arises across the cable and temperature distribution inside can either be measured by thermocouples or calculated by a numerical model. Fig. 1 shows an equivalent thermal circuit for the cable, where:
Q, heat transfer rate (heat flow), W;
θc, θcs, θi, θis, θis, θamb, temperature of conductor, conductor screen, insulation, insulation screen, sheath and ambient, °C;
Δθcs, Δθi, Δθis, temperature drop across conductor screen, insulation and insulation screen respectively, K;
Δθc-is, temperature difference from conductor to insulation screen, K;
Tcs, Ti, Tis, thermal resistance of conductor screen, insulation, insulation screen respectively, K·m/W;
Ts, thermal resistance in total from metal sheath to over sheath, K·m/W;
Ttm, thermal resistance of external thermal insulation material, K·m/W;
Temperature difference across conductor screen, insulation and insulation screen is calculated as follows:
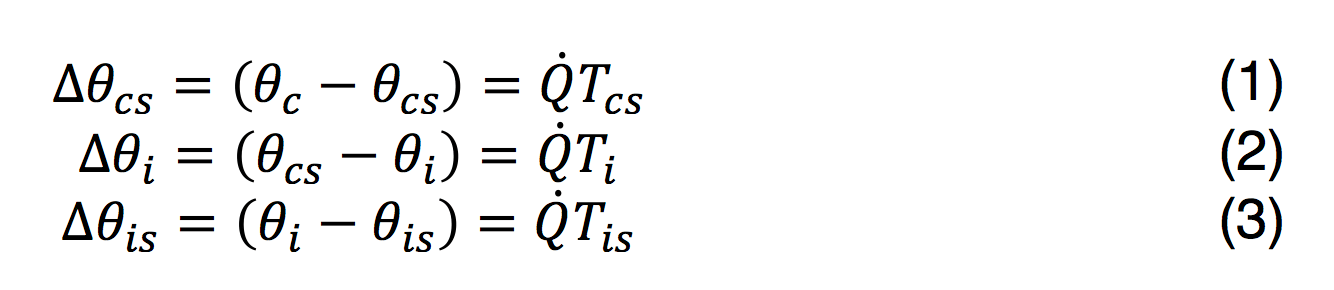
θis, and θc are measured directly by thermocouples. Overall temperature difference from conductor to insulation screen is therefore:
![]()
Based on Eq (2) and (4),
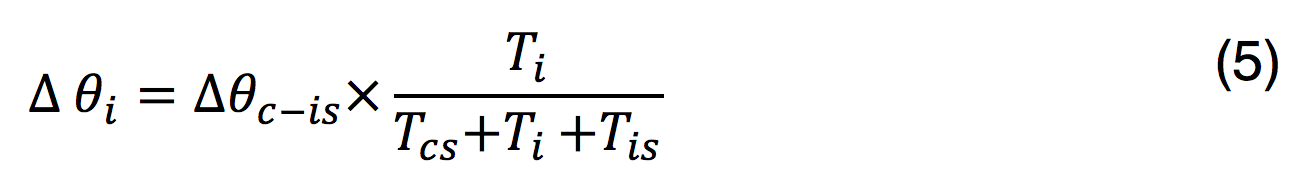
Eq (5) is the simple formula for calculation of ∆θmax. Since the surroundings also play a role, the main temperature drop in a cable is between the cable surface (sheath) and environment (θs-θamb). In order to control ∆θi within the limit of ∆θmax, external thermal insulation material (e.g. plastic bubble) is applied to minimize influence of the environment. This thermal insulation material helps adjust Ttm based on different cable design and surrounding condition.
Load Cycle & Temperature Measurement
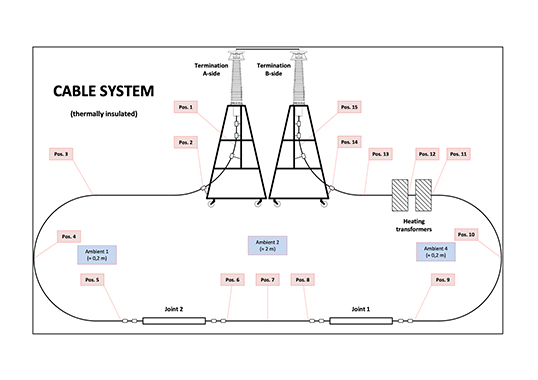
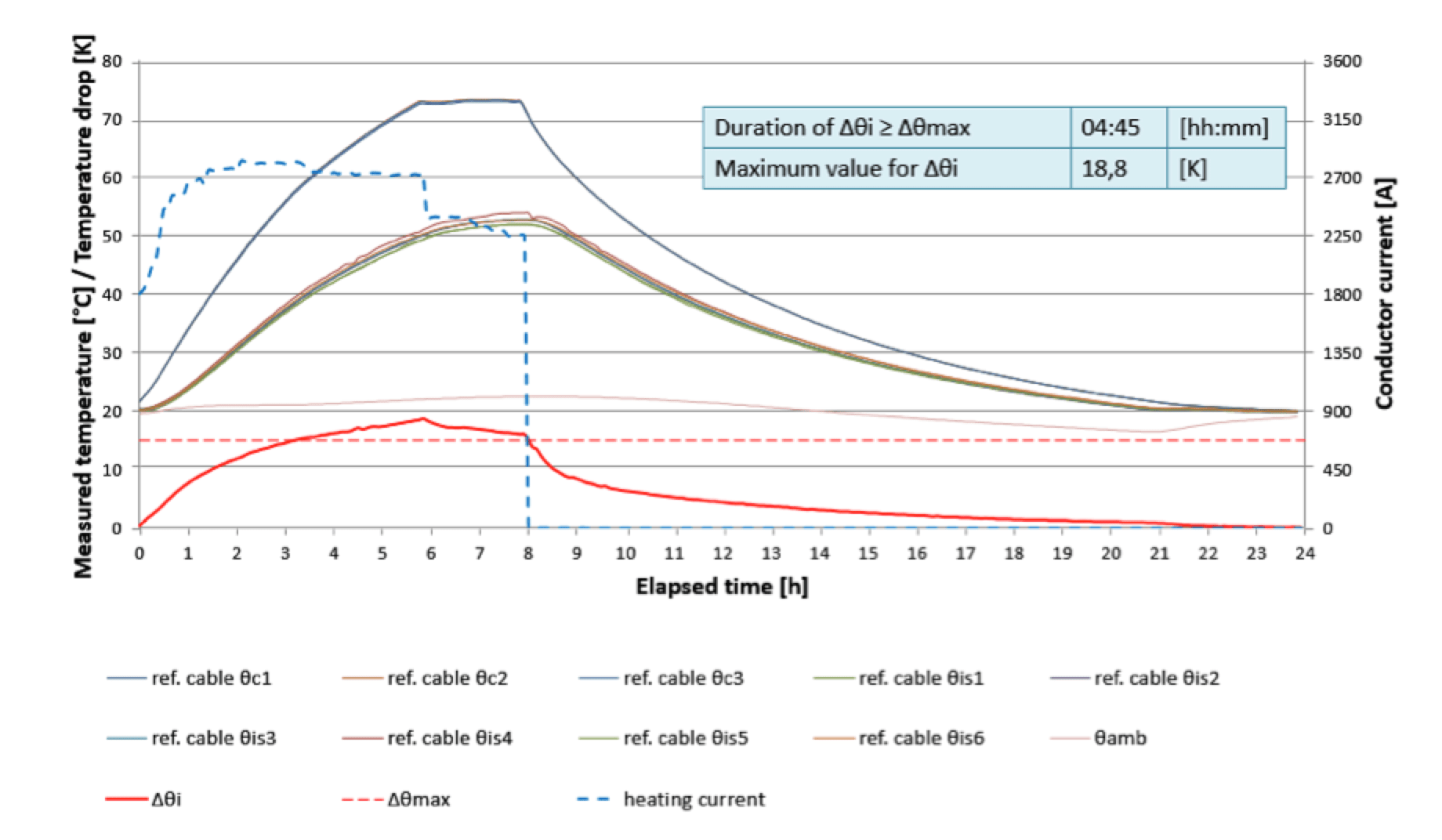
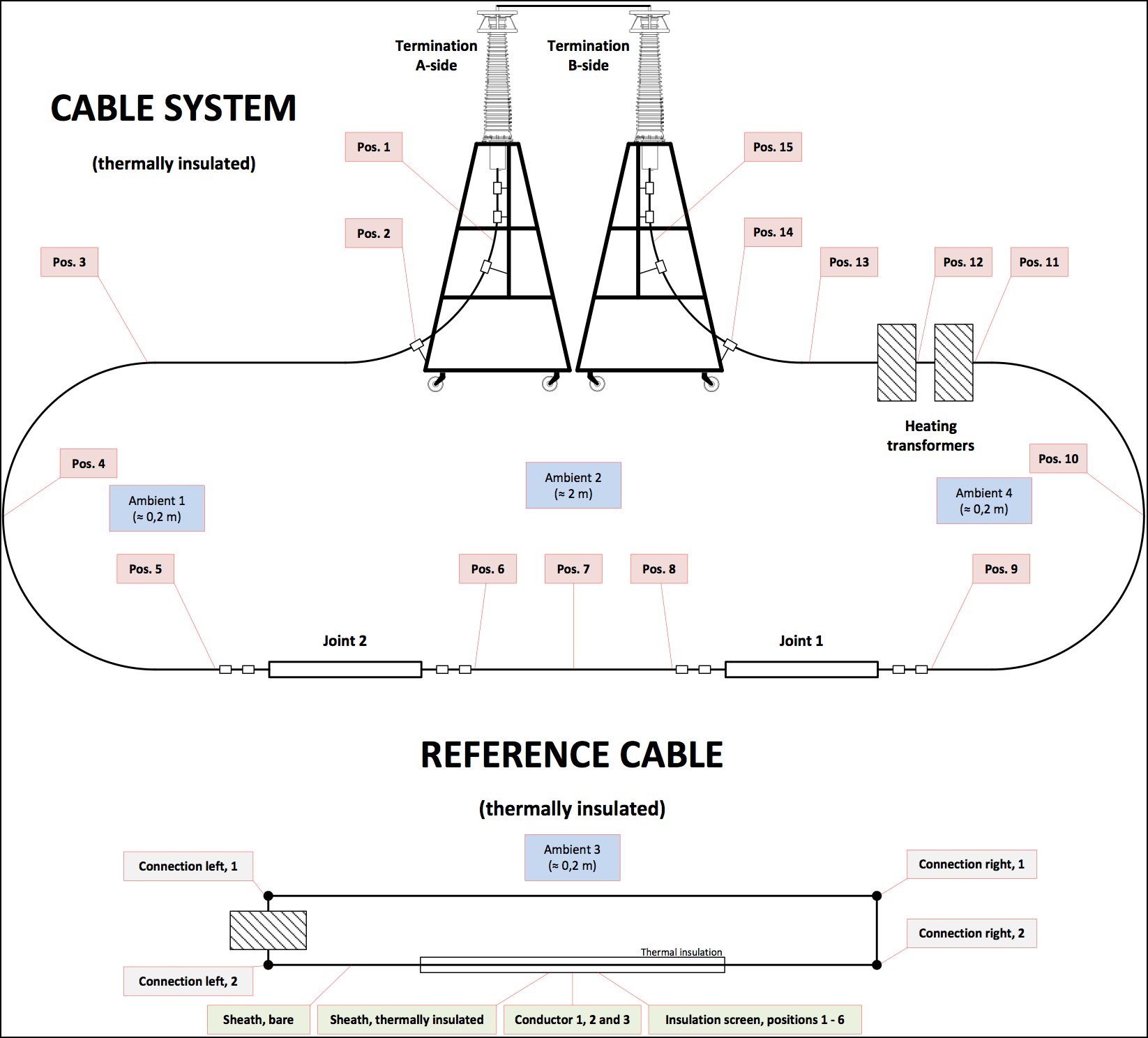
In order to monitor the thermal environment of HVDC cable system, thermocouples were placed at a total of more than 20 different locations on a reference cable and a test cable. The reference cable must be installed in close proximity with the test cable to ensure equal thermal environment. Conductor temperature of the reference cable (based on rated maximum θc, e.g. 70°C) was monitored to guide the same current applied to the test cable simultaneously. By applying Eq (5), specified Δθmax was calculated and monitored during the load cycle. Fig. 2 shows a typical 24 hours load cycle.
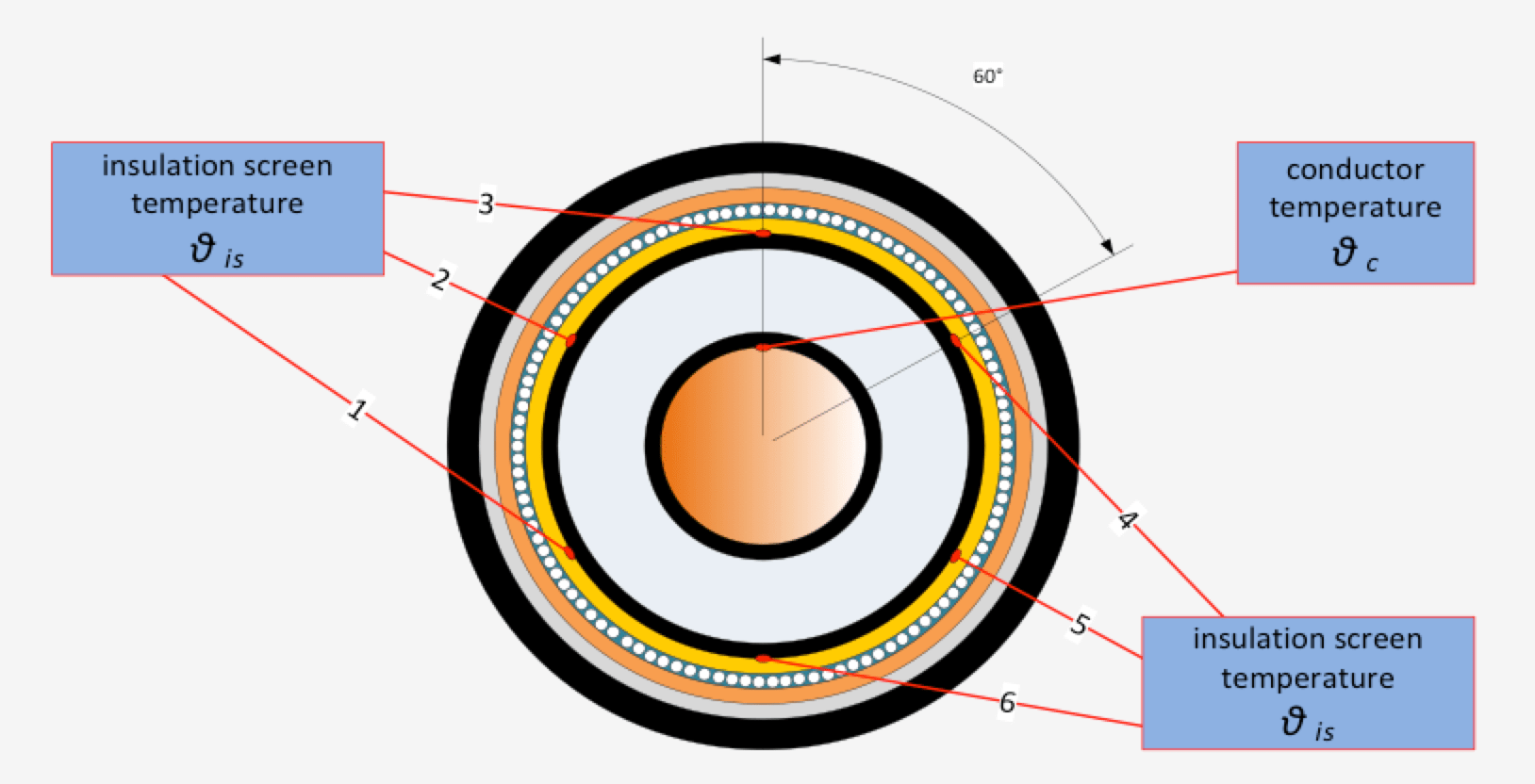
Figs. 3 and 4 schematically demonstrate the cable cross-section (e.g. 2500 mm2) and the locations of the measured temperature respectively.
Experimental Set-up
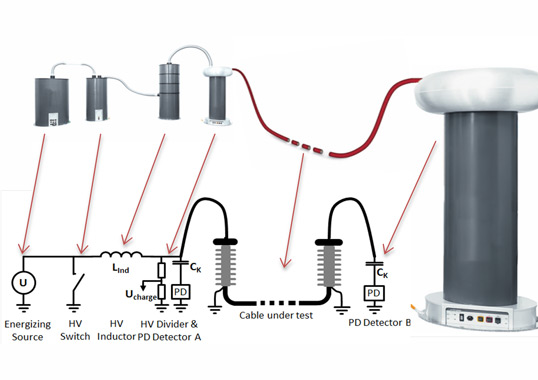
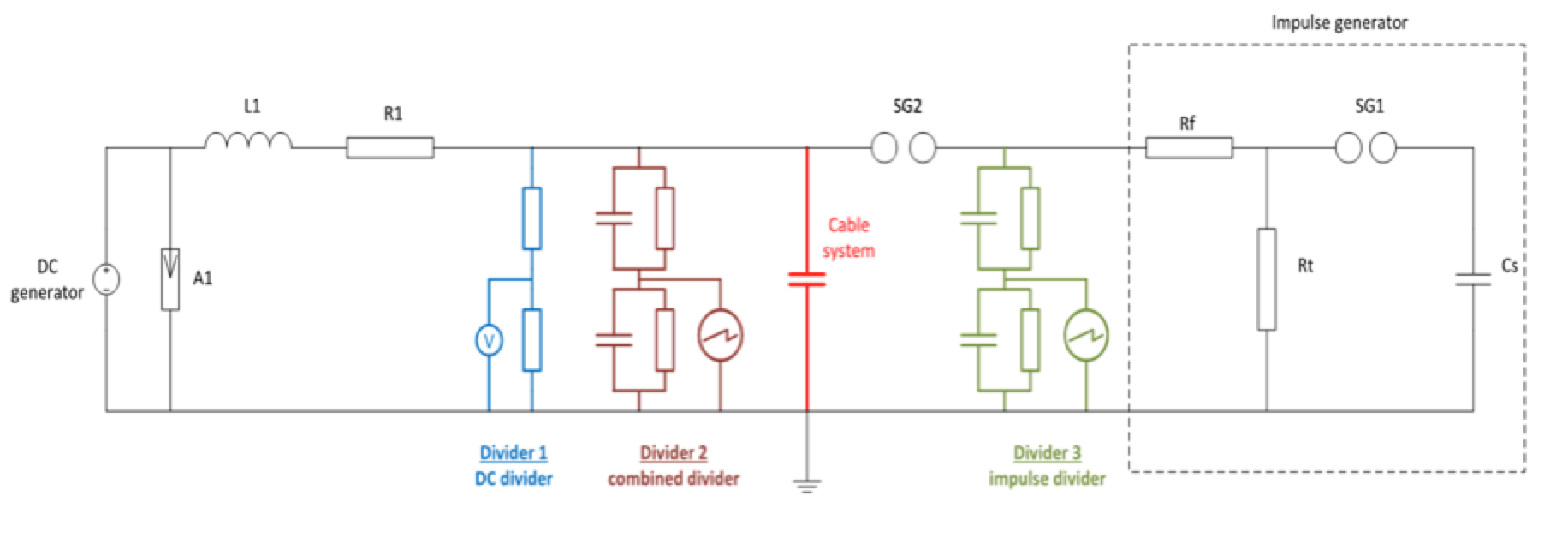
An experimental setup included a DC generator, an impulse generator and a test object, which was a 320 kV DC cable system including HVDC XLPE cable (copper conductor and XLPE insulation, nominal capacitance of 0,26µF/km), two outdoor oil terminations and two premoulded joints with shield interruption. A schematic test circuit and a photo of a real test setup are shown in Figure 5 and Figure 6 respectively. Each test system was equipped its own divider in order to measure DC voltage (Divider 1 in Fig. 5) and SI/LI (Divider 3 in Fig. 5) respectively. A combined divider (Divider 2 in Fig. 5) was applied to measure the superimposed withstand voltage subjected directly to the test object.
A pair of spheres (diameter of 0,5 m, SG2 in Fig. 5) was installed in vertical position, the lower sphere directly fixed to the outdoor terminations. The DC generator was also connected to the lower sphere with the protection water resistor (10 MΩ, R1 in Fig. 5) and the blocking impedance (35 mH, L1 in Fig. 5) in between. The upper sphere was separated from the lower sphere and the cable by an air gap and connected to the impulse generator. The surge arrestor (A1 in Fig. 5 ) was installed for extra protection of the DC generator

Test Procedure
Accurate measurement of voltage waveforms and self-ignition of sphere gap are the two essential aspects for a superimposed impulse test. By means of a sphere gap, this gap must ignite at a certain level and transfer the SI/LI to the cable system. The gap distance has to be considered and adjusted. Under the same polarity of two voltages (e.g. + UDC and + USI, a unipolar stress), the breakdown voltage of the sphere gap (Ubd unipolar = UDC – USI ≥ UDC , thus USI ≥ 2 UDC), in contrary to a bipolar stress (e.g. + UDC and – USI), the voltage (Ubd bipolar = UDC – (– USI) ≥ UDC , thus absolute USI ≥ 0). Therefore under the bipolar stress, there is not critical for breakdown the air gap; however under the unipolar stress, it is a complex procedure due to the Ubd unipolar. Furthermore, this calibration steps are necessary to avoid overshot of the test object [4]. The distance of sphere gap needs to be adjusted corresponding with the calibration of impulse voltages from low scales (50%, 65% and 80% of the test voltage) up to full scale (100% of the test voltage).
Analysis of Measured Results
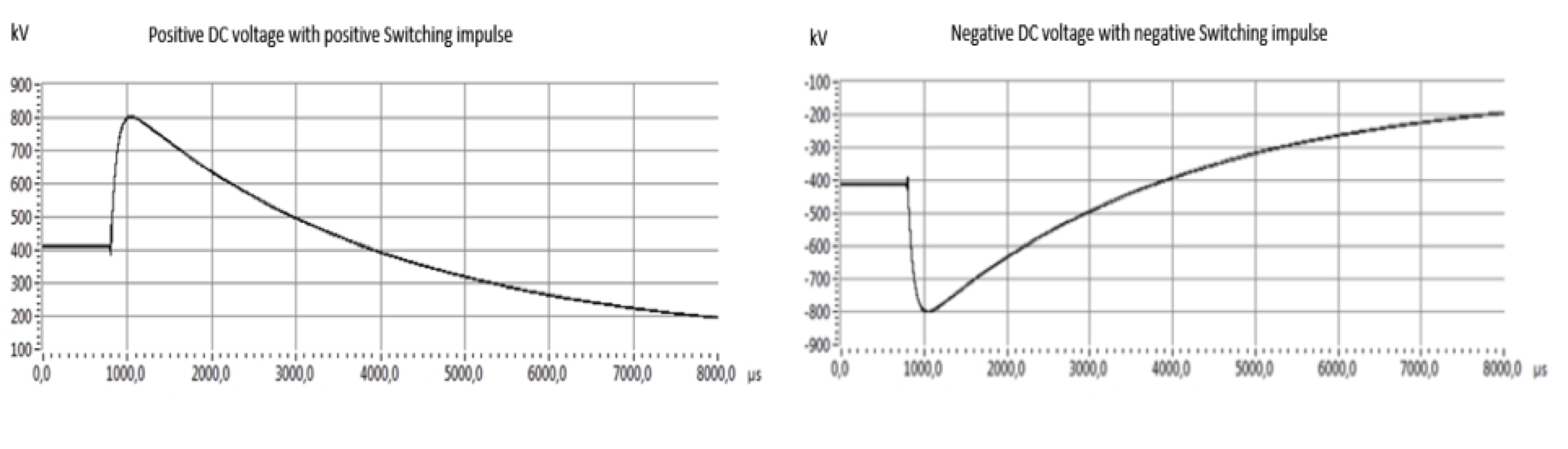
The three measured voltages were obtained with three dividers D1, D2, D3 (see Fig.5) during the testing. The DC voltage measured by the Divider 1 via a digital voltage meter and the full scale of DC voltage should be 320kV. The SI/LI voltages were overserved by the Divider 3 and the peak voltages should be 710kV and 740kV respectively (see Fig.7). DC voltage superimposes with same polarity of SI is shown in Fig. 8. It is further found that DC voltage superimposes with opposite polarity SI and LI in Figs, 9 and 10 respectively.
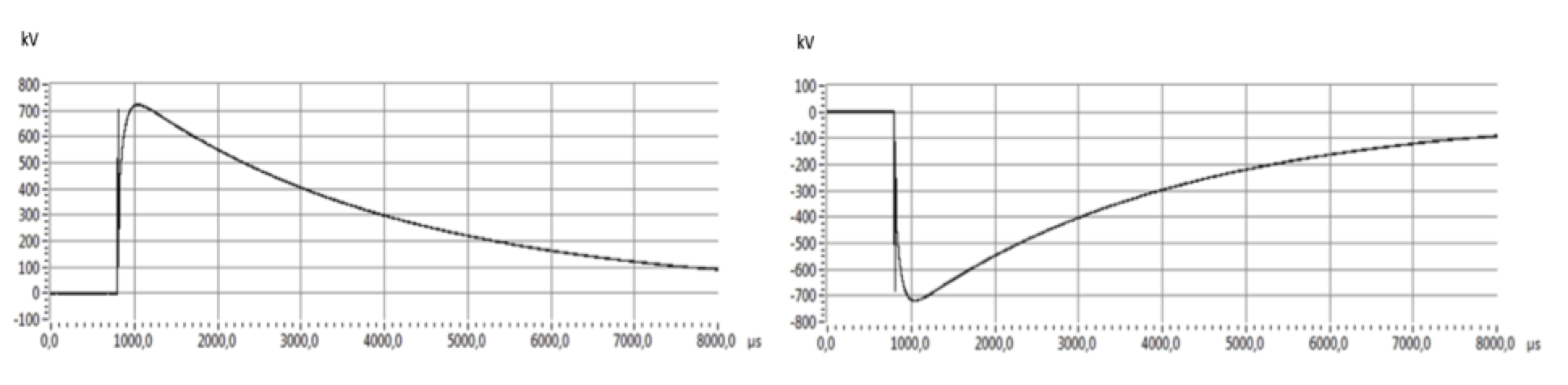
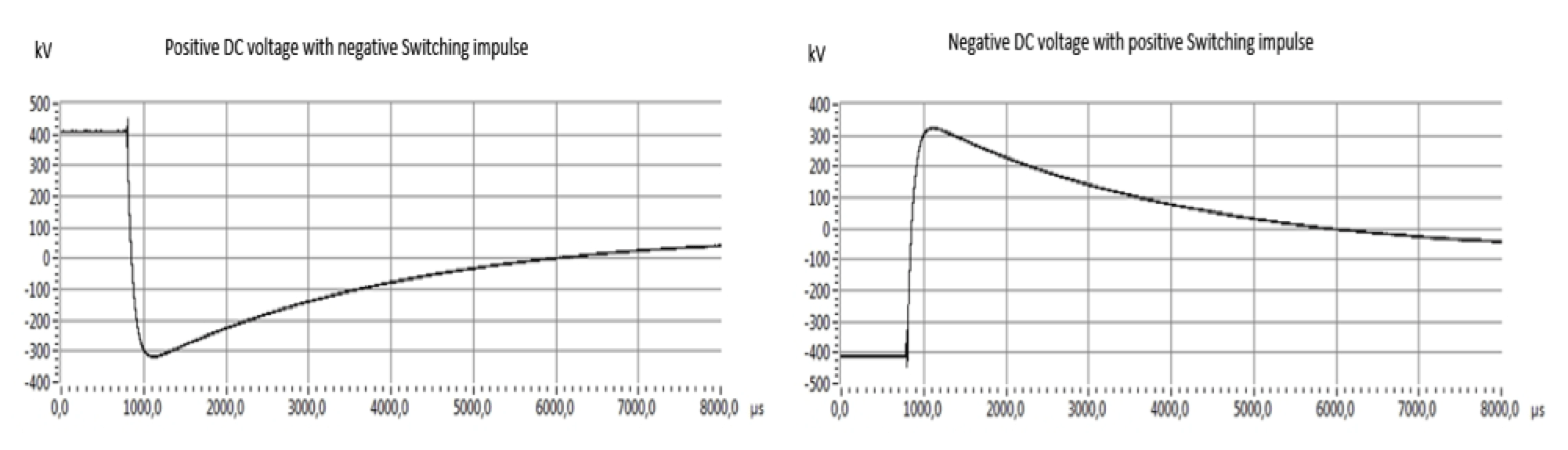
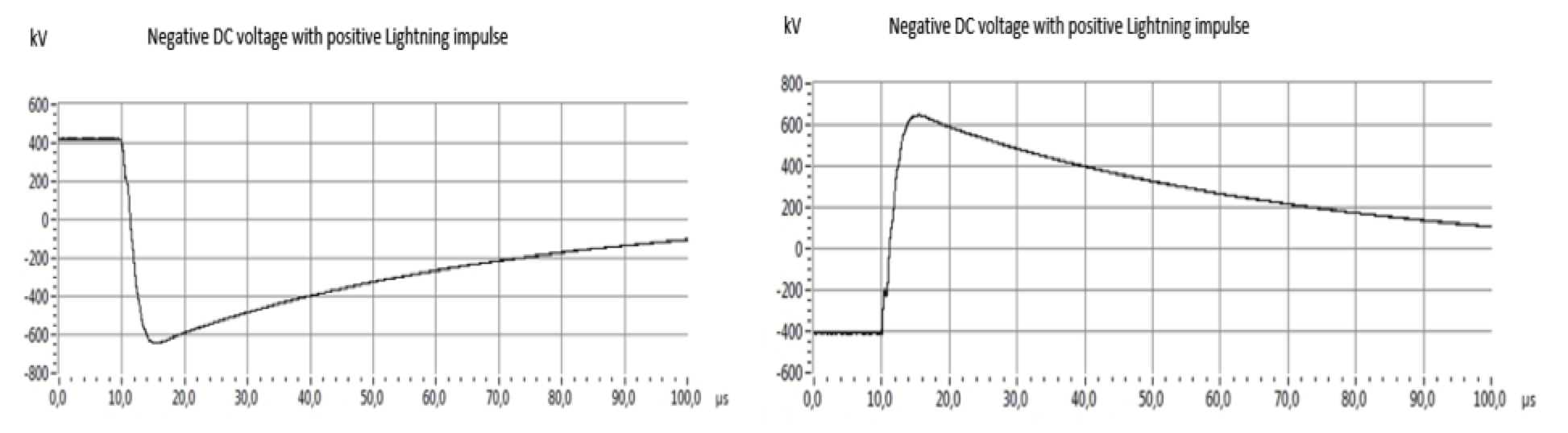
In Fig. 7, the Divider 3 measured a spike in front of the SI wave shape, which is the time delay of the protection sphere gap, it was until over the breakdown voltage, then sphere gap was conducting and the cable system was connected at that moment to the impulse generator.
It is observed in Fig. 8, a systematic DC offset error occurs during the tests. The Divider 2 was calibrated by DC voltage and Impulse voltages respectively. For combined voltages, a correction factor is needed (i.e. a factor of 0,78). This offset leads to a difference of peak voltages of impulses measured by Divider 3 and Divider 2.
It is noticed that, once the arc between the spheres was ignited, the voltage on the cable system followed the voltage at the terminal of the impulse generator. Thus the voltage on the cable system in extreme short time (hundreds or thousands of µs) discharged via impulse generator to extinguish voltage of the arc (visible in graphs), then it would take short recover time (few hundreds of ms) to recharge to the DC voltage (invisible in graphs due to limitation of data collection). In the meantime, the protection resistors sustained the full difference of impulse voltage and DC test voltage.
Conclusions
The calculation of Δθmax is obtained based on heat transfer method. In order to maintain a constant surface temperature of the cable, needed to guarantee a specified Δθmax , the practice methods are to control load current through conductor, maintain constant ambient temperature or apply the external thermal insulation material.
A proper test setup using a sphere gap has been developed for the application of SI/LI superimposed on a DC voltage. The correct gap adjustment is essential for unipolar stress condition, otherwise under certain circumstances, the high-frequency oscillations might occur.
Further experimental work focused on a method of controlling cable sheath temperature and developing a new three-channel software with extended data capture time (up to recover time of DC voltage). Moreover, a protection capacitor is another alternative of a sphere gap to realize the superimposed withstand test.]
Attend the 2023 INMR WORLD CONGRESS in Bangkok, where experts from across the globe will discuss key issues in cable commissioning testing and condition monitoring. These include: